Аналоговые часы с использованием Arduino Pro Mini, DS3231, Nokia 5110 и математики

Немного вводной части

Цифровые часы - это часы, которые просто показывают цифры для обозначения времени, например, 20:56. Сигнал от модуля часов реального времени (RTC) (DS3231), подключенного к Arduino pro mini и дисплею Nokia 5110, отображает время в цифровом формате.

Аналоговые часы - это часы, которые показывают время с помощью циферблата и расположеных на нем стрелок, часовой и минутной, иногда бывает еще и секундная стрелка.

В данном материале пойдет речь о том, как преобразовать цифровой сигнал из модуля часов реального времени в аналоговый формат с использованием тригонометрических функций, таких как синус и косинус.

Расчеты будут выполняться с помощью кода, загруженного в Arduino Pro Mini (3,3 В, 8 МГц). Проект рассчитан на питание от литий-ионной батареи 18650, которую можно извлечь из батарейного блока старого ноутбука или купить в магазине. Модуль TP4056 будет использоваться в качестве зарядного устройства для батареи.

В качестве справки для понимания каждого отдельного расчета в конце статьи будет ссылка  на файл Excel с пояснениями и значениями. 

Если изучая тригонометрию в школе, вы когда-либо спрашивали себя, пригодится ли она вам, то вот вам пример.  

Список деталей

• Arduino pro mini (3,3 В, 8 МГц)
• Дисплей Nokia 5110
• RTC DS3231
• аккумулятор либо батарея тип  2032 3,6 В 
• Модуль зарядного устройства TP4056 Micro USB 5V 1A
• Аккумулятор Li-Ion TP4056 3,7 В 
• Батарейный отсек для 18650
• Кабель для макетной платы
• Комплект соединительных проводов
• Макетная плата 400 отверстий
• Макетная плата 170 отверстий
• Микропереключатель
• Однорядный штекер с удлинителем 17 мм

Теория

Конечно для учета времени, есть возможность использовать встроенную функцию millis (), но как только вы отключаете питание, произойдет сброс и придеться начинать заново. Таким образом, в конечном итоге вы интегрируете в свой проект внешний модуль часов реального времени (RTC). В этом проекте часы реального времени DS3231 используются вместе с аккумулятором.

Для отображения времени был использован недорогой монохромный ЖК-дисплей от Nokia 5110, поскольку он работает при напряжении 3,3 В, то литий-ионная батарея вполне для этого подойдет. Так же дисплей имеет низкое энергопотребление, и библиотеку легко найти в интернет. Библиотека «LCD5110_Graph» была загружена с веб-страницы Rinky-Dink Electronics. Библиотека предоставляет функцию с именем «drawLine (x1, y1, x2, y2)». Эта функция позволяет нарисовать линию между двумя точками. Это именно то, что нам нужно что бы нарисовать стрелки аналоговых часов.

Теперь рассмотрим вопрос в том, как перевести цифровой сигнал (например, 9:25) в графическое представление показывающее время в аналоговой версии.

Общая идея заключается в том, что дисплей имеет разрешение 84x48 пикселей, что в свою очередь будет являться нашей декартовой системой координат. Декартова система координат - это система координат имеющая совокупность одной, двух, трех или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, – начала координат – и единичных отрезков на каждой из осей.

Каждый пиксель на дисплее Nokia можно описать с помощью числовых координат в системе 84x48. В качестве иллюстрации добавлена картинка для визуализации осей X и Y. Значение для осей у дисплея указываются от 0 до 83 (84 пикселя) для оси X и от 0 до 47 (48 пикселей) для оси Y. Функция «myGLCD.drawLine (0, 0, 83, 47)» рисует линию от верхнего левого угла до нижнего правого угла.

Поэтому угловые точки наших стрелок часов могут быть описаны числами (точками) в декартовой системе координат. С помощью функции drawLine из библиотеки мы можем соединить эти угловые точки, чтобы сформировать стрелку часов.

Расчеты

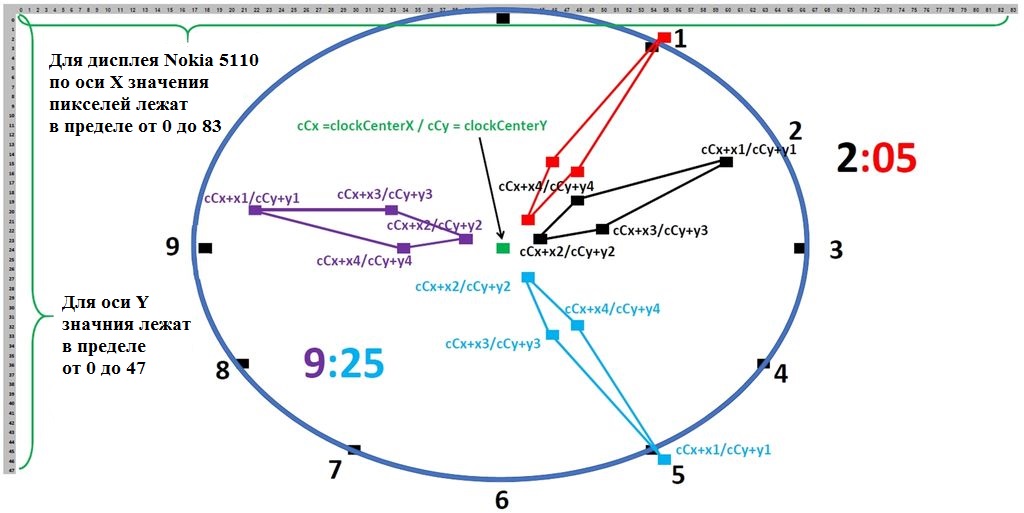
На рисунке стрелки часов обозначены линиями разного цвета, которые отображают два разных времени (9:25 и 2:05). Четыре угловые точки соединены четырьмя линиями, образуя стрелку часов. Для времени 2:05 (черный цвет) часовая стрелка описывается следующими координатами:

1. Точка: cCx + x1 / cCy + y1
2. Точка: cCx + x2 / cCy + y2
3. Точка: cCx + x3 / cCy + y3
4. Точка: cCx + x4 / cCy + y4

Почему эти координаты выглядят такими сложными, когда на самом деле вам нужны только два числа для описания точек? Это потому, что мы используем центральную точку в наших часах, а именно ClockCenterPoint (cCx = clockCenterX / cCy = clockCenterY). Причина выбора этой контрольной точки заключается в том, что вся информация в часах с круглым циферблатом может быть получена только из центра. Давайте расчитаем центральную точку.

Центральная точка:

cCx = половина оси x - при использовании дисплея Nokia половина из 84 равна 42

cCy = равна половине оси y - при использовании дисплея Nokia половина 48 равна 24

Так что на данный момент у нас есть следующие координаты для точки 1: 42 + x1 / 24 + y1

Расчет X1 и Y1

Голубой ромб на картинке является изображением часовой стрелки, например, показывает два часа. Мы определили центральную точку как начало отсчета (см. зеленую точку на рисунке). Чтобы использовать тригонометрические функции, нам нужно нарисовать прямоугольный треугольник, включающий в себя центральную точку и двухчасовую точку. Этот прямоугольный треугольник обозначен пунктирными линиями. Учитывая острый угол α [альфа] (обозначен желтым цветом на рисунке) прямоугольного треугольника, гипотенуза (hhe = часовой конец гипотенузы) является стороной, которая соединяет два острых угла. Сторона, примыкающая к α, - это сторона треугольника, которая соединяет Y1 с прямым углом. Третья сторона (X1) называется противоположной Y1.

Тригонометрические функции, которые можно применить здесь: α= альфа.

sin α = противоположная сторона / гипотенузу

Если вы замените противоположную сторону на X1, а гипотенузу на hhe (конец часовой стрелки), вы можете решить следующее уравнение: sin α = x1 / hhe -> x1 = sin α * hhe

Переменная «hhe» обозначает длину часовой стрелки. При использовании дисплея Nokia 5110 половина из 48 пикселей составляет 24 пикселя. Опытным путем выяснилось, что значение 25 максимальная длина. Так как часовая стрелка должна быть немного короче минутной стрелки, примем для нее значение навное 20. Таким образом, меняем в уравнение hhe на 20:

x1 = sin α x 20

Теперь единственной неизвестной переменной остается угол. Угол зависит от цифрового значения времени, поступающего от модуля RTC, тогда мы получаем следующие: 360 градусов (это круг циферблата) делится на 12 частей (по кол-ву часов на циферблате) получаем 30 градусов в час.

Поскольку часовая стрелка также перемещается между часами, мы включаем:

30 градусов в час, разделенные на 60 минут = 0,5 градусов в минуту. Следовательно, угол можно рассчитать следующим образом:

α = (час * 30°) + (минута * 0,5°)

В нашем примере со временем 2:05 (см. Рисунок в шаге 4) мы получаем следующий угол: (2 x 30) + (5 x 0,5) = 62,5°

х1 = sin 62,5*20

При решении тригонометрических выражений, таких как синус или косинус, важно понимать, что Arduino IDE использует радианы, а не градусы для выполнения этих вычислений! Если угол в градусах, вы должны сначала преобразовать его в радианы. Чтобы преобразовать градусы в радианы, возьмите число градусов, которое нужно преобразовать, и умножьте его на число (ПИ) π / 180. При проверке кода для Arduino (см. Шаг 10) вы найдете выражение π / 180, замененное на 0,0175.

Общее: x1 = sin (α / 180 x π) x hhe

Пример со временем 2:05: x1 = sin (62,5 / 180 x π) x 20 -> x1 = 18 для часовой стрелки (файл Excel для расчета)

То же самое для Y1 только при использовании функции косинуса и отрицательного значения (из-за ориентации в системе).

Общее: Y1 = -cos (a / 180 x π) x hhe

Пример с 2:05: Y1 = -cos (62,5 / 180 x π) x 20 -> y1 = -9 для часовой стрелки

1. Точка: cCx + x1 / cCy + y1: 42 + 18/24 - 9 -> 60/15 (первые координаты часовой стрелки).

Статья находится в стадии написания